Tutoriel Prédictif
Le prédictif dans DigDash Enterprise est présent à travers trois fonctionnalités :
- Les mesures prédictives
- Les mesures simulées
- Le groupement intelligent
Ce document illustre une utilisation possible de ces différents outils.
Mesures prédictives
Création d'une mesure prédictive
L'accès à la création d'une mesure prédictive s'effectue via l'interface de Configuration avancée de la source de données (voir image ci-dessous) :
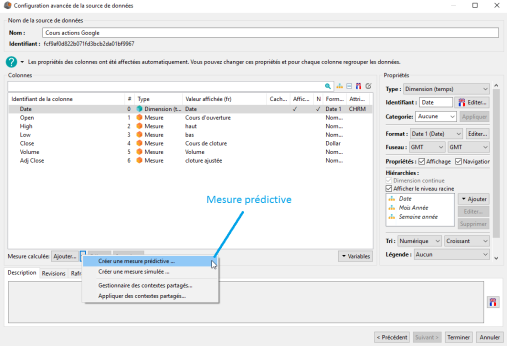
Pour créer une mesure prédictive il suffit de cliquer sur Créer une mesure prédictive..., ce qui a pour effet d'ouvrir la fenêtre Mesure prédictive.
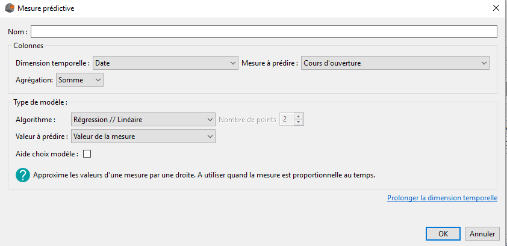
La création d'une mesure prédictive s'effectue via la fenêtre ci-dessous et implique de renseigner plusieurs champs obligatoires :
- Le nom de la mesure prédictive
- La mesure que l'on souhaite prédire
- La dimension temporelle selon laquelle on souhaite explorer notre mesure
- L’agrégation de la mesure à prédire
- Le type de modèle/algorithme. Pour chaque algorithme, nous précisons dans quel contexte il est intéressant/pertinent de l'utiliser. De plus, en cochant la case Aide choix modèle nous aidons l'utilisateur à déterminer un modèle à utiliser en fonction de la nature des données qu'il souhaite prédire.
- Le type de valeur que nous souhaitons prédire. DigDash Enterprise offre la possibilité de prédire soit la valeur de la mesure, ou bien les bornes de l'intervalle de confiance à 95 % de la prédiction.
Modèles disponibles et choix du modèle
DigDash Enterprise intègre 9 modèles de prédiction que nous présentons dans le tableau ci-dessous :
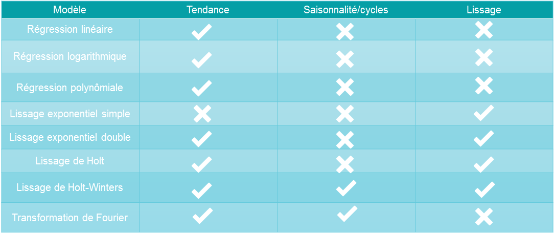
DigDash Enterprise intègre également un algorithme de moyenne mobile, mais celui-ci n'est pas un algorithme de prédiction à proprement parlé car il permet seulement d'étudier les données du passé.
Le choix du modèle de prédiction dépend de la mesure que l'on souhaite prédire et du type de modélisation que l'on souhaite faire. Il est important de se poser les questions suivantes :
- Mes données possèdent-elles une tendance ?
- Mes données possèdent-elles une saisonnalité ou bien des cycles ? Si oui, sont-ils complexes ?
- Est ce que je souhaite lisser mes données?
- Est ce que je veux obtenir une modélisation simple de mon problème, facile à visualiser, ou bien je souhaite favoriser la précision du modèle au détriment de sa simplicité.
Grâce à son interface d'aide au choix de modèle (voir image ci-dessous), DigDash Enterprise restreint le choix de modèles disponibles en répondant aux deux premiers points.
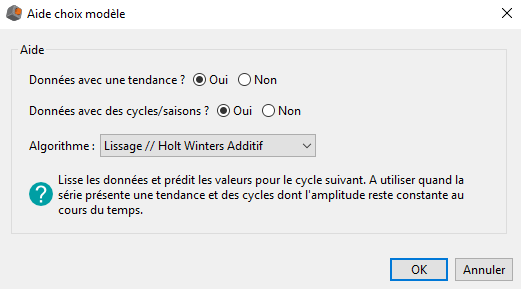
Dans la prochaine partie nous présentons les différents modèles plus en détails afin d'en faciliter la compréhension par l'utilisateur.
Présentation des modèles
Les définitions des algorithmes ci-après sont à considérer dans le cadre des mesures prédictives au sein de DigDash Enterprise.
Régression linéaire :
La régression linéaire est un des outils de base de la modélisation. Elle recherche une relation linéaire entre la mesure à prédire et l'axe temps.
La situation d'application idéale de ce modèle est lorsque la mesure à prédire est proportionnelle à l'axe temps. Toutefois, il peut être également intéressant de choisir ce modèle pour sa simplicité de visualisation (une droite), ce qui le rend rapidement compréhensible par un large public.
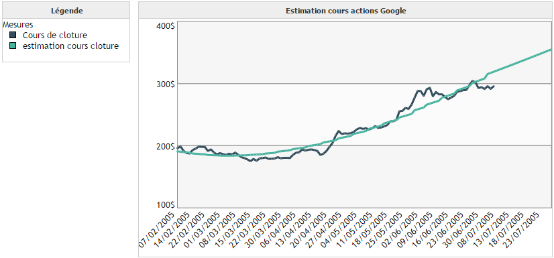
Exemple 1 :
On souhaite modéliser le cours de clôture de l'action Google en fonction du temps.
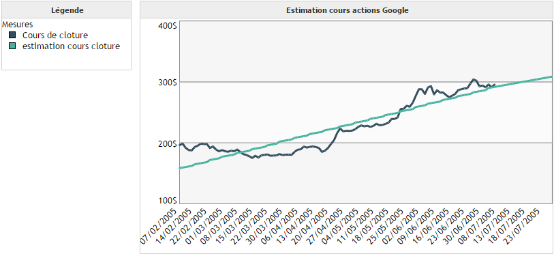
On remarque que la prédiction via la régression linéaire n'est pas très précise dans ce cas. Toutefois, elle permet de visualiser rapidement l'évolution de la tendance de la courbe.
Exemple 2 :
On souhaite modéliser l'évolution du chiffre d'affaires d'une société en fonction du temps.
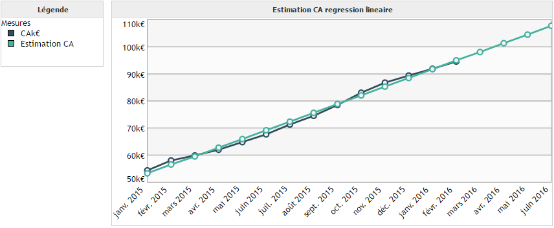
Dans cet exemple nous sommes dans le cas idéal d'application de la régression linéaire. En effet, il existe une relation de proportionnalité entre le chiffre d'affaires et le temps.
Régression logarithmique :
La régression logarithmique possède les mêmes propriétés que la régression linéaire. La différence réside dans le fait qu'elle permet de trouver une relation logarithmique entre la mesure à prédire et l'axe temps.
Exemple :
Régression polynomiale :
La régression polynomiale est une forme plus complexe de la régression linéaire. Elle permet d'approximer une mesure non plus par une droite mais par un polynôme d'ordre 2 ou 3.
Exemple :
Moyenne mobile :
L'objectif de la moyenne mobile n'est pas de prédire, mais de lisser les données afin d'éliminer les fluctuations les moins significatives. Une moyenne mobile d'ordre 3 par exemple est une moyenne glissante qui pour chaque point p, calcule la moyenne des points p-1, p et p+1. Dans ce cas, le calcul de la moyenne mobile n'est possible qu'à partir du deuxième point jusqu'à l'avant dernier.
Exemple :
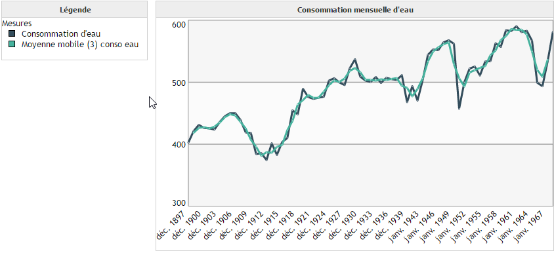
On peut observer que la moyenne mobile d'ordre 3 a permis de lisser la courbe de consommation d'eau. Cela permet de supprimer les variations brutales comme en 1953 afin de se concentrer sur l'allure globale de la courbe.
Lissage exponentiel simple :
Contrairement aux techniques de régressions qui ne sont pas propres aux séries temporelles, les lissages tiennent compte de la spécificité de la variable temporelle. En effet, l'importance à donner à une valeur décroît dans le temps. Par exemple, pour prédire le chiffre d'affaires de l'année 2017, il est probable que l'on donne plus d'importance à la valeur du CA de 2016 qu'à la valeur du CA de 2008. Les diverses techniques de lissages permettent donc de tenir compte de la dépréciation de l'information au cours du temps.
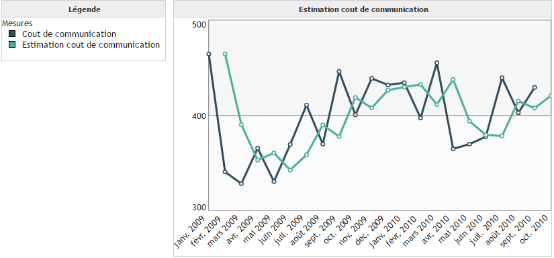
Le lissage exponentiel simple permet à la fois de lisser des données et également de prédire la prochaine valeur. Il s'applique à des données ne présentant ni tendance et ni saisonnalité.
Exemple :
On cherche à prédire le coût de communication en fonction du temps. On remarque que les données sont assez chaotiques : elles n'ont ni tendance et ni cycle. C'est une situation où la prédiction est assez complexe. C'est la raison pour laquelle l'algorithme de lissage exponentiel simple effectue seulement une prédiction pour la prochaine date.
Lissage exponentiel double :
Le lissage exponentiel double est une version améliorée du lissage exponentiel simple car celui-ci est capable de prendre en compte la présence d'une tendance dans les données. Toutefois, il ne permet pas de prédire des données présentant une saisonnalité.
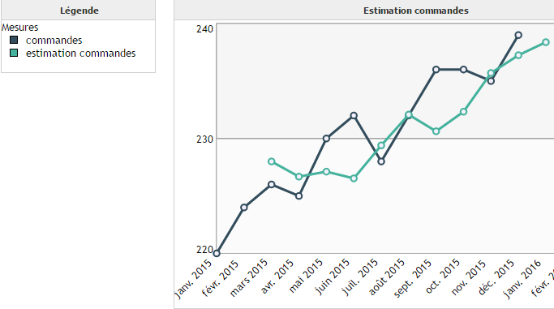
Exemple :
On cherche à prédire le nombre de commandes d'un fournisseur en fonction du temps. En observant nos données on remarque que celles-ci présente une tendance, mais pas de saisonnalité. On réunit dans les conditions d'application du lissage exponentiel double.
Lissage de Holt :
Le lissage de Holt est une version améliorée du lissage exponentiel double. Celui-ci utilise deux paramètres afin d'estimer la valeur de la mesure, contre un seul pour le lissage exponentiel double.
On peut alors se demander pour quelle raison utiliser le lissage exponentiel double si le lissage de Holt est plus précis. La raison principale est le temps de calcul. En effet, dans le cas du lissage de Holt il faut estimer deux paramètres, contre un seul dans le cas du lissage exponentiel double.
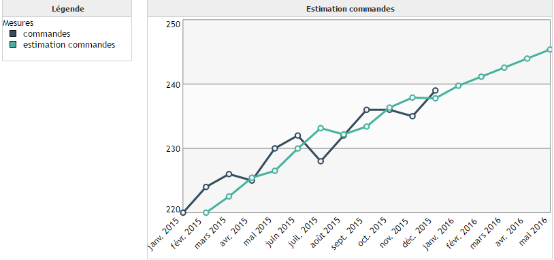
Exemple :
Nous utilisons les mêmes données que pour le lissage exponentiel double car les conditions d'applications sont les mêmes.
Lissage de Holt-Winters :
Les lissages de Holt-Winters permettent de prendre en compte des données présentant une tendance et une saisonnalité.
DigDash Enterprise implémente deux versions du lissage de Holt-Winters :
- Version additive
- Version multiplicative
Le cas additif correspond à des saisons dont l'amplitude reste constante au cours du temps (voir image ci-dessous) :
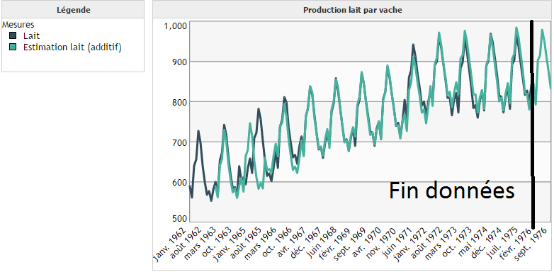
Le cas multiplicatif correspond à des saisons dont l'amplitude croît/décroît au cours du temps (voir image ci-dessous) :
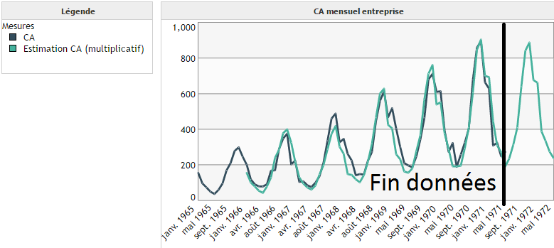
Contrairement au premier exemple (cas additif), on observe que l'amplitude des cycles augmente au cours du temps. D'où l'intérêt d'utiliser un modèle multiplicatif et non plus additif.
Transformation de Fourier :
L'algorithme permettant de prédire la mesure n'est pas la transformation de Fourier, c'est un algorithme de prédiction utilisant la transformation de Fourier.
Techniquement, l'objectif est de décomposer la mesure à prédire en une somme de fonction sinus et cosinus de périodes différentes. Grâce à cela, notre algorithme est capable de prendre en compte des cycles/saisonnalités plus complexes que celles présentées dans la partie sur les modèles de Holt-Winters.
Exemple :
Pour cet exemple nous souhaitons prédire le nombre de maisons vendues au sein d'une agence immobilière. En observant les données nous remarquons une forme de cyclicité au sein de celles-ci. Toutefois, elle n'est plus aussi simple que celles des exemples de la partie sur les modèles de Holt-Winters.
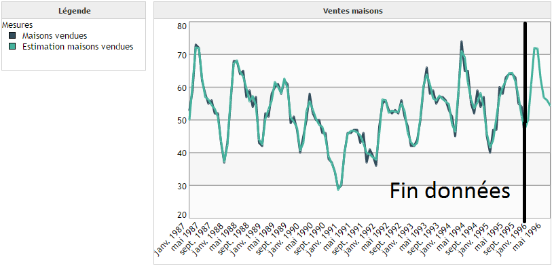
Valeurs à prédire
A travers les mesures prédictives nous proposons de prédire 3 valeurs :
- La valeur de la mesure
- Borne inférieure de l'intervalle de confiance à 95 %
- Borne supérieure de l'intervalle de confiance à 95 %
L'intervalle de confiance est défini de telle sorte que la valeur prédite a 95 % de chance d'être comprise entre les deux bornes.
Attention, ce résultat n'est valable que lorsque les données sont normales (au sens gaussien du terme). Toutefois, même si cette hypothèse n'est pas respectée, il peut toujours être intéressant visuellement de tracer les intervalles de confiance.
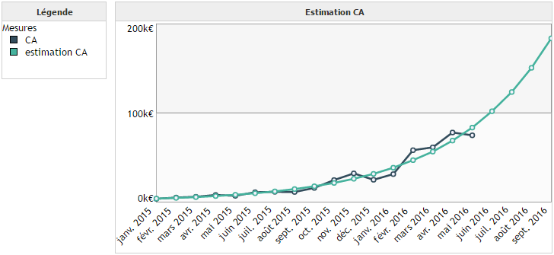
Exemple :
Nous utilisons les intervalles de confiance sur notre premier exemple de régression linéaire appliquée au cours de l'action Google.
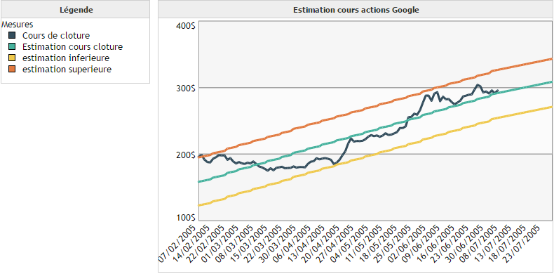
Considérations mathématiques
Dans le cas des algorithmes ne possédant pas de solutions mathématiques exactes, les paramètres sont approximés en cherchant à minimiser la somme des erreurs au carrées (SSE).
Le nombre d'itérations pour estimer ces paramètres n'est pas modifiable par l'utilisateur actuellement.
De plus, il est important de comprendre que les algorithmes présentés précédemment se servent du passé pour prédire les valeurs futures. Cela implique plusieurs points :
- Plus il y a de données, plus la prédiction sera précise
- Les algorithmes se basent sur le passé, ils considèrent que le futur sera similaire à celui-ci. Par conséquent, ils ne sont pas capables de prédire des chocs structurels
- L'exactitude des prédictions ne peut être garantie et n'est pas à prendre d'un point de vue déterministe.
Mesures simulées
Une mesure simulée a pour objectif d'étudier l'influence d'une ou plusieurs mesures sur une autre mesure.
Création d'une mesure simulée
L'accès à la création d'une mesure simulée s'effectue via l'interface de Configuration avancée de la source de données (voir image ci-dessous) :
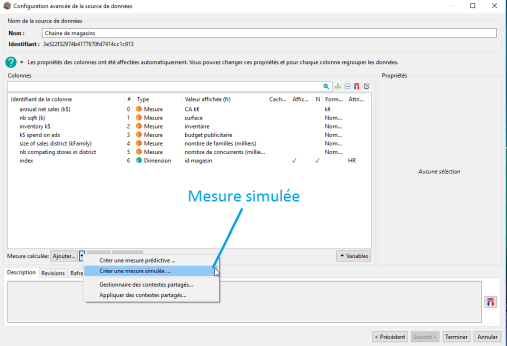
Pour créer une mesure simulée il suffit de cliquer sur Créer une mesure simulée, ce qui a pour effet d'ouvrir la fenêtre Mesure simulée.
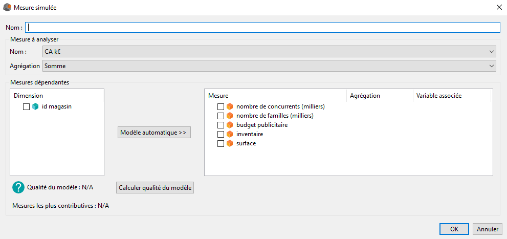
Ensuite, il faut renseigner les informations suivantes :
Entrez le nom que vous souhaitez donner à votre mesure simulée.
Dans le groupe Mesure à analyser vous devez sélectionner :
- La mesure que vous souhaitez analyser
- L'agrégation de cette mesure
Dans le groupe Mesures dépendantes vous devez sélectionner les mesures que vous souhaitez faire intervenir pour modéliser la mesure à analyser. Pour chaque mesure vous devez renseigner deux autres informations :
- L'agrégation de la mesure
- La variable associée à cette mesure. Si vous ne souhaitez pas faire varier la mesure, sélectionnez Aucune.
Les autres champs présents dans le groupe Mesures dépendantes sont facultatifs. Nous allons toutefois expliquer leur utilité.
Le bouton Modèle automatique permet de sélectionner automatiquement les mesures permettant de modéliser la mesure à analyser. Pour cela vous devez également sélectionner la ou les dimensions selon lesquelles vous souhaitez explorer les mesures afin de déterminer le modèle.
Le bouton Calculer qualité du modèle permet de calculer le coefficient de détermination ajusté (R² ajusté). Celui-ci calcule la précision du modèle tout en tenant compte de la complexité de celui-ci. Pour cela vous devez sélectionner les mesures de votre modèle, ainsi que leur agrégation, et également la ou les dimensions selon lesquelles vous souhaitez explorer les mesures afin de calculer la précision.
Exemple
Notre exemple portera sur une chaîne de magasins. Nous disposons des données suivantes pour chacun des magasins :
- CA annuel
- Surface
- Stocks (k€)
- Budget publicité (k€)
- Nombre de familles dans un rayon de 30km (milliers)
- Nombre de concurrents dans un rayon de 30km
Tout d'abord nous allons commencer par étudier l'effet du budget publicitaire sur le CA annuel.
Pour cela nous allons créer une mesure simulée en renseignant les champs comme dans l'image ci-dessous :
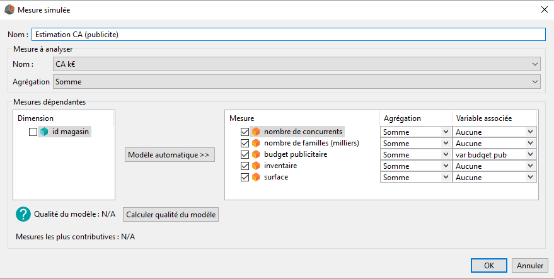
Nous avons sélectionné toutes les mesures car nous voulons toutes les utiliser pour modéliser le CA de nos magasins. Toutefois, comme nous souhaitons tester seulement l'influence du budget publicitaire, nous avons laissé la valeur variable associée à Aucune pour l'ensemble des mesures autres que budget publicitaire.
La variable associée à la mesure budget publicitaire est la variable var budget pub. Cette variable est une variable classique comme on peut en utiliser dans les mesures calculées.
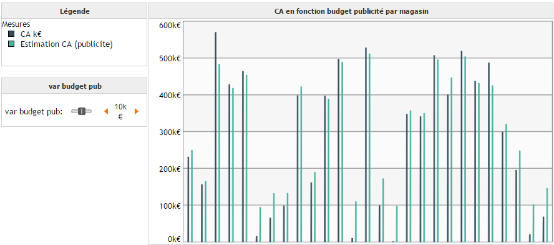
Une fois la mesure simulée créée, on peut réaliser un graphique en barres sur lequel on positionne les mesures CA ainsi que notre nouvelle mesure simulée, groupées par magasin. Dans le tableau de bord nous ajoutons notre variable var budget pub afin de pouvoir faire varier sa valeur, et ainsi observer son influence sur Estimation CA(publicité).
Modèle mathématique
Les mesures simulées utilisent la régression linéaire multiple afin de modéliser la relation entre la mesure à analyser et les mesures dépendantes. Cela signifie que DigDash Enterprise n'est pas capable de modéliser automatiquement des relations d'ordre non linéaire. Toutefois, l'utilisateur peut appliquer des transformations sur ces données manuellement soit via les transformateurs de données, soit via les mesures calculées.
De plus, à l'instar des mesures prédictives, il est important de comprendre que les algorithmes présentés précédemment se servent du passé pour prédire les valeurs futures. Cela implique plusieurs points :
- Plus il y a de données, plus la prédiction sera précise
- Les algorithmes se basant sur le passé, ils considèrent que le futur sera similaire à celui-ci. Par conséquent, ils ne sont pas capables de prédire des chocs structurels
- L'exactitude des prédictions ne peut être garantie et n'est pas à prendre d'un point de vue déterministe.
Groupement intelligent (clustering)
Création d'un groupement intelligent
Le groupement intelligent (clustering), permet de grouper les membres d'une dimension selon certaines mesures. L'objectif est de grouper les membres « similaires ». La notion de similarité est à interpréter au sens mathématique du terme, c'est à dire des membres qui ont des valeurs proches pour des mesures données.
Dans la section Hiérarchies, cliquez sur Ajouter puis Groupement intelligent. La boîte Groupement intelligent s'affiche.
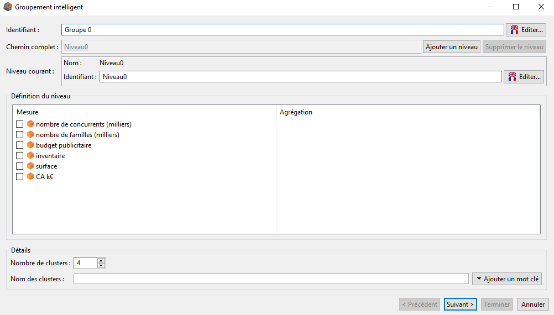
La partie supérieure de la fenêtre est similaire à cella de création d'une hiérarchie manuelle. On peut y définir l'identifiant de la hiérarchie (par défaut Groupe 0), y ajouter des niveaux, et changer l'identifiant des niveaux.
Les différences se trouvent dans les groupes Définition du niveau et Détails.
Dans le groupe Définition du niveau on définit selon quelles mesures nous souhaitons grouper les membres du niveau courant. Pour cela, vous devez cocher les mesures selon lesquelles vous souhaitez grouper vos membres. Pour chacune de ces mesures vous devez également sélectionner son agrégation.
Le groupe Détails permet de renseigner deux éléments :
- Le nombre de clusters (nombre de groupes) du niveau courant
- Le nom de ces clusters
Le nom des clusters peut être composé de différents mots clés que l'on introduit grâce au bouton Ajouter un mot clé situé en bas à droite de la fenêtre.
Les mots clés proposés par DigDash pour nommer les clusters sont les suivants :
- ${bestMeasures} qui permet de nommer les clusters selon les 3 mesures qui différencient le plus les différents groupes. Chaque nom de cluster sera donc de la forme Mesure1Position,Mesure2Position,Mesure3Position où la position est comprise entre 0 et nombre de clusters du niveau, et indique comment la moyenne de la mesure se positionne par rapport à celle des autres groupes (pour plus de détails voir l'exemple ci-après).
- ${Measure(nomMesure)} qui permet de choisir soit même les mesures que l'on souhaite faire intervenir dans le nom des clusters
Par défaut le nom des clusters est égal à ${bestMeasures}.
Attention, il n'est pas possible de combiner ${bestMeasures} avec ${Measure(nomMesure)}.
L'utilisateur a également la possibilité d'insérer du texte personnel dans le nom des clusters.
Pour finaliser la première étape de la création du groupement intelligent l'utilisateur doit cliquer sur le bouton Suivant. Cela a pour effet de déclencher le calcul des groupes et de l'amener à une seconde fenêtre, identique à celle de création d'une hiérarchie manuelle, mais dont les groupes sont déjà constitués.
Cette seconde étape est donc totalement identique à la création d'une hiérarchie manuelle. Vous avez exactement les mêmes possibilités que dans ce cas. Pour plus de détails, se référer à la partie sur la création d'une hiérarchie manuelle.
Exemples
Exemple 1 :
Nous disposons de données sur les magasins d'une chaîne de supermarchés. Nous souhaitons créer 5 groupes de magasins similaires en terme de budget publicitaire et de chiffre d'affaires. Nous sélectionnons le mot clé ${bestMeasures} pour nommer les groupes (clusters) de magasins.
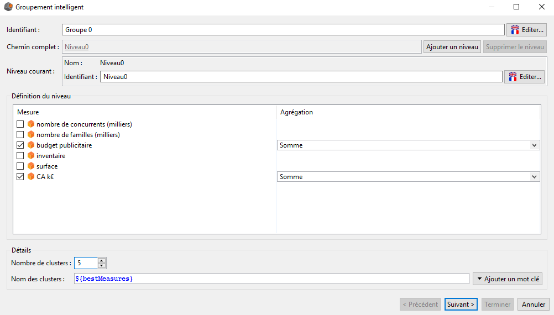
En cliquant sur le bouton suivant nous obtenons le résultat ci-dessous :
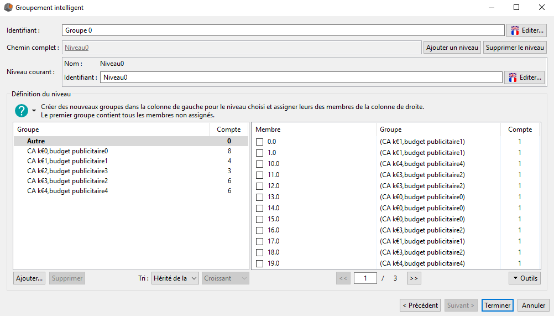
Nous obtenons 5 groupes de magasins comme demandé à l'étape précédente. Le nom des groupes est de la forme Cak€Position,budget publicitairePosition.
Pour le groupe CAk€0,budget publicitaire0 cela signifie que ce groupe est constitué des magasins ayant le chiffre d'affaires et le budget publicité le plus bas (position 0). Le groupe CAk€4, budget publicitaire4 quant a lui est constitué des magasins ayant le chiffre d'affaires et le budget publicité le plus élevé.
Exemple 2 :
Nous disposons de données sur des vins :
- Qualité du vin (moyenne de notes d'utilisateurs)
- Indicateurs chimiques (pH, degré d'alcool, densité, etc)
Nous souhaitons grouper nos vins en quatre groupes, à la fois selon leur qualité, mais également selon leur degré alcoolique.
Pour cela nous complétons l'interface Groupement intelligent de la manière suivante et nous cliquons sur le bouton Suivant :
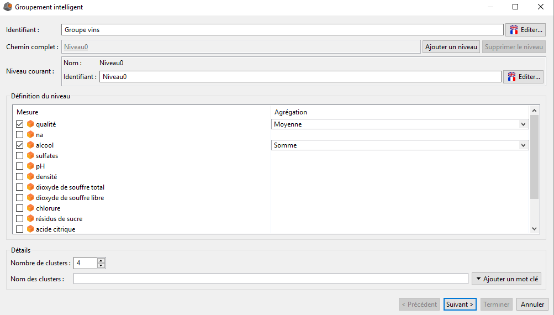
Dans l'interface suivante nous validons la création de notre hiérarchie.
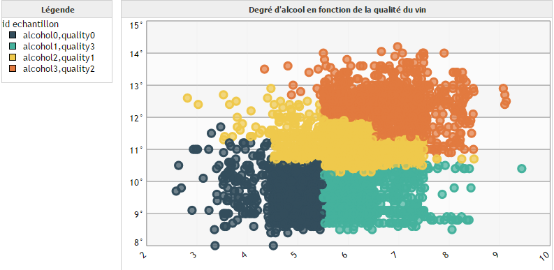
Ensuite, nous créons un graphique de type Scatter. Sur l'axe Y nous positionnons le degré alcoolique du vin, sur l'axe X la qualité de ceux-ci. Dans le champ Bulles nous plaçons notre dimension id échantillon, qui correspond aux identifiants de nos vins. Nous la laissons au niveau racine. Pour le champ Cycler les couleurs nous plaçons également la dimension id échantillon, sauf que cette fois nous nous mettons au niveau 0 de notre hiérarchie.
Nous obtenons la représentation graphique suivante :
Considérations mathématiques
Les groupes (clusters) sont déterminés grâce à l'algorithme Kmeans++ dont le résultat dépend des paramètres d'initialisation. Ainsi, si vous relancez plusieurs fois la création de groupement intelligents avec les mêmes paramètres, il est normal que vous n'obteniez pas exactement les mêmes résultats.